素数の浪漫 第2弾はRSA暗号の仕組みについて解説する。RSA暗号は素数の素因数分解の困難さを利用した暗号化方式だ。そもそも素数とは何か。素因数分解の困難さについては第1弾の記事をチェックしてほしい。
素数の浪漫 第1弾 ~素数とはなにか~
では、素数を利用したRSA暗号についてみていこう。
暗号化の必要性
暗号化はセキュリティの面で非常に重要な通信の仕組みだ。
我々はインターネットで日々、様々な情報をやり取りしている。そこには個人情報やパスワードなどの認証情報も含まれている。ここで悪意の持った第3者が通信を盗聴した時、その内容が平文(暗号化等、整形されていない元の文章)だとすると盗聴者に情報が漏洩することになる。
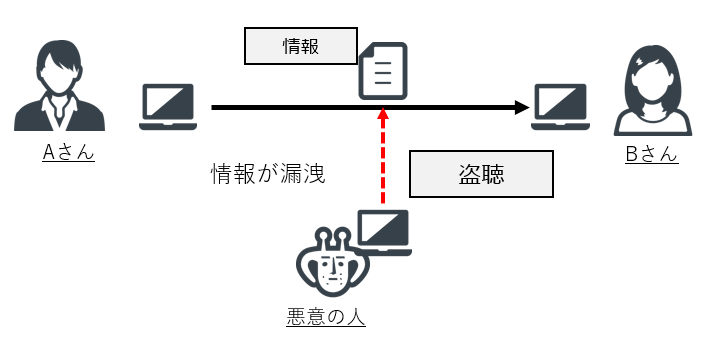
そこで、情報を暗号化します。思想としては盗聴されても内容は解読できず受け取り手(上図のBさん)のみが暗号化された情報の復元が可能になる、という考え方になる。
暗号化の仕組み
暗号化の仕組みとしてはこうだ。
1.受け取り手(以下Bさん)は秘密鍵と公開鍵を生成する。
2.Bさんは公開鍵を配布する。秘密鍵は公開せずBさんのみ知っている状態。
3.送り手(以下Aさん)は配布された公開鍵によってBさんへ送りたい情報を暗号化する。
4.暗号化された情報を受け取ったBさんは秘密鍵によって情報を復元し平文を確認する。
この時、Bさんの公開鍵によって暗号化された情報はBさんのみが知る秘密鍵でのみ複合化が可能である。通信の傍受により悪意のある人に情報が盗聴されても秘密鍵がなく復元化が困難なので情報が漏洩することはない。
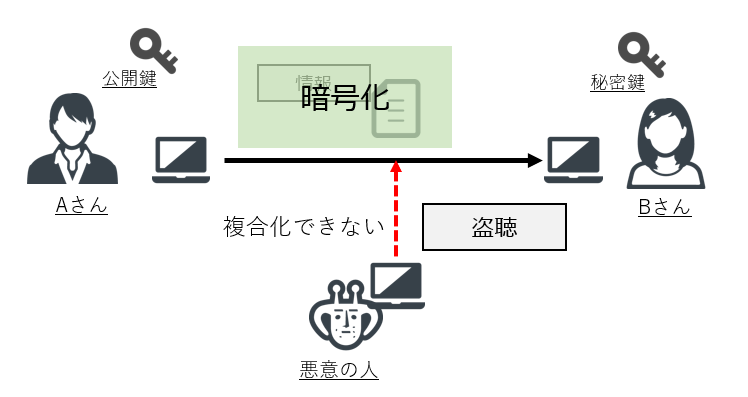
公開鍵を配布するということは、誰でも暗号化してBさんへ情報を送ることは可能だが、その内容は情報を送る人と、その暗号化された内容を復元できるBさんのみ知ることができるということである。
このようにして、現代の情報化社会は我々の情報を悪意のある人から守っているのだ。
では、この仕組みの中で「素数」はどのように利用されているのだろうか。
素数を利用したRSA暗号化
ここからは少々数式を交えて説明する。まず用意するのは2つの大きな素数p,qだ。
さらに、その積である合成数 N ≡p × q を生成する。ここで重要なのは、用意した素数p,qを知らなければ合成数Nを素因数分解することは非常に困難である、ということだ。
素因数分解の困難さについては、第1弾の記事に寄り道してほしい。
素数の浪漫 第1弾 ~素数とはなにか~
1.公開鍵を生成する
Bさんは公開鍵を生成する。
最初に用意した大きな素数p,qについて、用意した合成数の他にもう1つ数を計算する。
更に、鍵穴に該当する値も求める。
ここからは、公開鍵は赤字、秘密鍵は青字としている。

ここまで用意しておくと、合成数N,と鍵穴e は公開鍵として公開できる。
受けとった情報の送り手は、この2つの値で暗号化することが可能だが、先に秘密鍵を準備しておこう。
2. 秘密鍵を生成する
公開鍵として生成した鍵穴e と素数p,qを利用して新しく用意したnを利用して、ある式を満たす値dを求めていく。

ここで mod は合同式といい、商(割り算)の余りを表す。
例えば、以下のように等式が成り立つ。
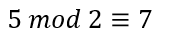
5と7は、どちらも2で割った余りが等しい(=1)という意味。
従って、2-1図は、鍵穴にある数値を掛けて、用意したnで割った時の余りが1となるようなある数値を求めよ、ということだ。このある数値dを秘密鍵として受け取り手は未公開で保管しておく。
3. 情報を暗号化する
情報の贈り手は、取得した公開鍵で以下のように暗号化を施す。

送りたい情報M、そして公開鍵N,e は送り手側で分かる情報であることが重要だ。
こうして作成された暗号文Cを受け取り手へ送信する。
4. 暗号文を複合化する
受け取り手は、受け取った暗号文Cを以下のように解読できる。

秘密鍵d は受け取り手しかしらないものだ。これと送られてきた暗号文C、更に合成数Nを利用して情報Mが複合化できる。重要なのは秘密鍵d は2つの大きな素数がわかれば作成できるが、その情報は受け取り手しか知らない。また合成数Nから元になった素数p,qを素因数分解から割り出すのは、大きな素数を用意しているため困難である。したがって安全に送り手から受け取り手へ情報の送信が可能になるのだ。
また、この複合が可能であることについては、自明ではない。ここでは省略するがオイラーの小定理などを利用して数学的に元の情報に戻ることが証明されている。
以上が素数を利用したRSA暗号の仕組みである。
さて、ここまで素数の基本的な性質、そして暗号として身の回りで利用されていることを見てきた。次は素数の最も神秘的で興味深い話となる「素数に規則性は存在するのか」についてまとめていきたい。


コメント