我々は「素数」について、何をしっているだろうか。
日本では小学生の時に素数を学習し、中学生では素因数分解で利用する。「2,3,5,7,11,・・・」と至ってシンプルな数字の羅列は、我々人類にとって非常に大きな意味を秘めている。筆者はこの数字にロマンを感じるのである。
素数について小学生、中学生の思い出しから日常でどのように利用されているか解説していこう。
さらに素数が秘める未知の魅力について考えていこう。
素数ってなんだっけ
素数とは、数学の「整数論」と呼ばれる分野で研究されており、
「2以上の自然数で、約数が1と自分自身しか存在しない数」のことである。
※自然数、整数、正数、約数は~
即ち、「2,3,5,7,11,・・・」といった数のことだ。
「1」は素数ではない
ちなみに「1」も素数としての性質を満たしていないのか、という疑問があるかもしれない。
様々な説明があるが、以下に2つ説明を上げておく。数学者には申し訳ないが、自分自身が何かで納得すればよいと思う。
素数の定義
定義だ、と言ってしまえばそれで終わりだが・・。
定義中に”約数が1と自分自身”の2つしかないと言っているから。冒頭では”2以上の自然数”と付け加えているが、約数が1と自分自身の2つしかいないと言っているので、1の約数は1のみであり、素数ではないと説明できる。
素因数分解の一意性
素因数分解の結果は必ず1通りとなる。
しかし1を素数としてしまうと素因数分解の結果が一意でなくなるのである。
以下のように1はいくつかけても1なので素因数分解の結果が1つにならないのだ。
したがって1は素数でないと言える。

補足)素因数分解の一意性について
素因数分解の一意性についてもう少し補足しておく。
素因数分解とは?
>ある正の整数を、素数の積の形であらわすこと
因数とは?
>ある数を掛け算であらわした時の、掛け合わしているそれぞれの数のこと
例) 20 = 4 × 5
掛け合わせている要素は素数でなくてもよい。
素因数とは?
>因数に”素”がつくことで、掛け合わしているそれぞれの数はそれ以上は分解できない数、
すなわち素数となる。
例) 20 = 2 × 2 × 5
掛け合わせている要素は素数。
一意性とは?
>ただ1つであること、ユニークであること。数学、科学ではよく使う言葉。
素因数分解の一意性とは?
素因数分解の結果については、算術の基本定理として以下を担保している。
※全ての正の整数は素数の積として(順番を除いて)一意に表せる。
即ち、素因数分解の結果は素数の積としてただ1つ(一意)になると言っている。
ちなみに定理と言っているので数学的に証明可能であるがここでは割愛する。
さて、少し脱線したが本題に戻ろう。
1と自分自身以外に割ることができない数字達、素数自体は一見シンプルで分かりやすく思える数字の羅列である。しかしそこには、とてつもないロマンとインパクトを兼ね備えているのだ。
日常に現れる素数
日常生活で素数を意識することは滅多にない。
教養としては、日本人なら中学生の時にその存在を知るのみだ。
そう、素因数分解と共に。
日常生活で素数は、実は通信の暗号化に対して利用されている。
その時に重要な性質が素因数分解の難しさなのだ。
素因数分解の難しさ
素因数分解の前に、まずはその逆、素数から正数を作ってみよう。
用意した素数は「3,5,11」だとすれば、答えは 3 × 5 × 11 = 165 だ。
解き方は「すべて掛け算する」だ。
素数をかけ合わせれば数を作れることが分かっていればいい。
ではその逆に数を素数に分解(素因数分解)してみる。
中学生の時に素因数分解の問題を解いたことがあるだろう。
では思い出していただこう。
<問題> 42 を素因数分解せよ
答えは「42= 237」である。
おそらく頭のなかで以下のような計算を行ったと思う。
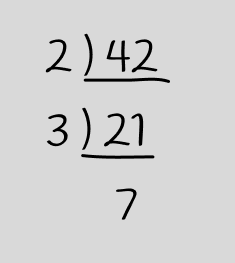
お気づきだと思うが、素数から数を作るより素因数分解の方が難しい。
しかも公式をゴリゴリ解いたり、論法のごとく型に当てはめて理論展開するものでもない。
ひたすら思いつく素数で割っていく作業なのである。
まさに”素数のゴリ押し”なのだ。
もう少し桁数を上げることで更に実感するだろう。
「3,5,11,23,59」を掛けると「223905」 (これは容易)
「127839」を素因数分解すると 「3*43*991」 (これは難しい)
この、素数から数を作る難しさ << 素因数分解の難しさ という性質が
世の中の暗号化技術に応用されている。
今回はここまでにしよう。次回はこの素数の性質が応用されたRSA暗号について解説する。



コメント