素数の浪漫 第1弾、第2弾では、素数の基本知識の復讐やRSA暗号への応用について解説してきた。
おそらく最終章になる第3弾は、ついに素数の未解決問題について足を踏み入れようと思う。
ここから内容が少々難儀になるが、なるべく分かりやすく解説していこうと思うのでお付き合い頂きたい。
素数への挑戦
バーゼル問題と素数と円周率の関係
バーゼル問題とは、平方数、すなわち2乗した数の逆数を無限に足し合わせるといくつになるか、という問題だ。

平方和の逆数の無限和については、1644年に出題されてから91年後の1735年にオイラーが解を導いた。証明については、ここでは割愛するがマクローリン展開と因数分解を軸に証明できる。
さらにこのバーゼル問題についてオイラーの功績がもう1つある。それは素数との結び付けだ。
全ての数は素数の合成数によって作られることから、素数の逆数和の積を展開すると以下のようになる。

如何だろうか。素数が円(π)、すなわち自然界で最も美しい形と結びついた式だ。
なにか素数には自然界との間に特別な関係があることを疑ってしまう。
素数の階段
1、2、3、4、5、6、7、8、・・・と自然数を数えていくと突如素数が姿を表す。
始めは、2、そして次に3、1つ飛ばして5、10数えるまでに2,3,5,7の4つの素数が存在する。
10を超えると11,13,17,19の4つが20までに存在する。ところが30台になると31、37の2つしか現れない。100を数えると現れる素数の個数は25になる。このように素数が出現する頻度は一見無秩序のように思える。
実際そうなのだが、これを視覚的にとらえるために素数の階段を考えてみる。
自然数の上を1から数えていくようにして歩いてみる。素数が現れれば1段階上がるような階段を描いてみるのだ。
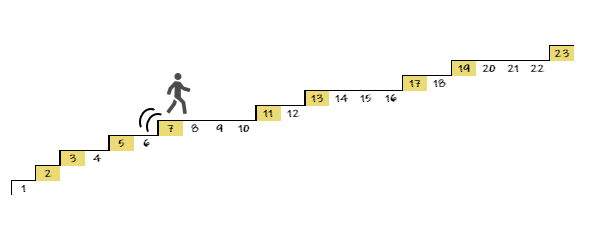
階段をよく見ると最初こそ順調に階段を上っているように見えるが、途中5個も素数が現れない箇所もあれば次の奇数で素数が出現する箇所もある。さらに大きい数まで考えると素数が100以上も現れない平坦な区間も存在する。
(これを素数砂漠というらしい。)
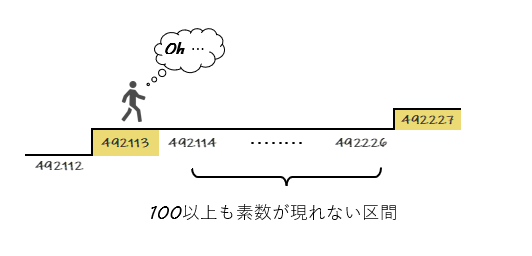
このように階段で見てみると素数の出現がいかに気まぐれか、視覚的にお分かりいただけただろうか。
しかし面白いことに、この素数に階段にはある性質が存在するのである。
素数定理
素数階段で見たように無秩序に現れる素数について、その分布を定式化して捉えることができないのか。実は、この命題こそが素数の未解決問題とされているのであるが、まずは、ある数までに含まれる素数の個数を見てみよう。
例えば10までに含まれる個数は「2、3、5、7」の4個である。

数が増えれば見つかった素数の累計は増えていくのは当たり前だが、増え方が緩やかに見ないだろうか。見つかった素数も、それ以上の数の素因数になるので見つかる素数が減っていくのは感覚でわかるだろう。実は、このある自然数を超えない素数の個数は、ガウスによって予想された素数定理によって与えられる。

“にょろ”の意味は左辺と右辺は漸近関係であることを表している。
(詳しくは左辺と右辺の比の極限が1になるということだが、単に”似ている”で捉えてよい。)
ある自然数に対して、素数定理から計算される理論値と実測値はこうだ。

精度は実測値と理論値の比で、ある自然数が大きくなるにつれて精度もかなり良いものになっていくことがわかる。ただし厳密に一致していないことに注意したい。すなわち素数定理を厳密に書くと誤差項を用いて以下のように表せる。
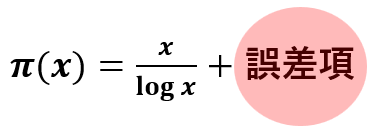
この誤差項が、素数の分布に対してより良い精度で書けるかのキーとなるのだ。
そして誤差項はゼータ関数の性質を調べることで決定できるのだ。
ゼータ関数
数学が苦手な方は既に何を言っているかわからないかもしれないが、何か壮大な物語の中に迷い込んでしまっていると感じていたら、それで良いと思う。ここまでいてくれて感謝である。
ゼータ関数の定義
ゼータ関数ζ(s)は以下のように定義される。
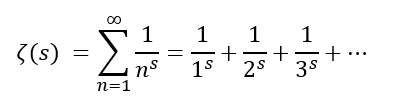
sはs>1の範囲で値をとる。要は自然数の変数s乗したものの逆数の無限和である。
ちなみにこの形はどこかで見たことがないだろうか。
そう、バーゼル問題と似た形なのだ。実際、s=2のゼータ関数はバーゼル問題に帰着するのである。
解析接続
次にゼータ関数を複素数に拡張する。複素数とは2乗してマイナスになる虚数iを導入し、2つ実数a,bに対して以下のように表すことが出来る数のことである。また実部R(z)と虚数Im(z)のように表記する。
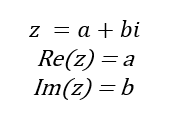
ある関数を実数だけではなく、この複素数の領域まで拡張することを解析接続という。もう少し丁寧にいうと、連続で微分可能になるように、滑らかに関数を延長し定義域を拡張する、と言える。ちなみに解析接続における関数の延長の仕方は、正則関数という性質上一意に決まる。これは非常に強力な性質である。こうしてゼータ関数を解析接続すると変数sが、s≠1の複素数全体で意味を成す。s=1はゼータ関数の極であり値を持たない特異点だ。さらにR(s)>1の範囲でゼータ関数は収束する。即ちゼータ関数はsの実部が1より大きいときのみ意味を持つ。以下にゼータ関数のいくつかの値を載せておく。

特にsが負の偶数の時、0をとり、これを自明な零点という。自明であるということは、数学的に当たり前であるということだが、一般人にその感覚はない。
一方、自明な零点に対して「 非自明な零点 」が存在する。この零点に関してある性質が予想されており、これをリーマン予想と呼んでいる。
素数公式
素数定理により、ある数までに含まれる素数の個数についての振る舞いは記述できる。しかし厳密な素数の個数を表すには誤差項を用いた。リーマンはこの素数の個数の振る舞いの式を解析接続により拡張したゼータ関数を用いて以下の式を導出した。
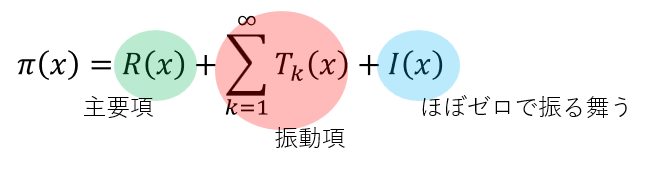
これをリーマンの素数公式という。ガウスの示した素数公式は、素数の個数を漸近的にしか表せなかったが、リーマンの素数公式は厳密な式で表している。
第1項の主要項は、ガウスの素数定理に近い振る舞いをし、第3項はほぼゼロで振る舞うためここでは解説を割愛する。そして第2項の振動項は、素数定理でも触れた誤差部分であり、以下のように表す。
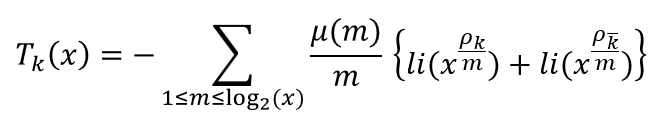
対数積分liに含まれるρはゼータ関数の非自明な零点を表している。すなわち振動項は零点の足し合わせにより、表すことで素数の個数π(x)の値を厳密に決定することへ寄与しているのである。
リーマン予想
リーマン予想の主張とわかっていること
さて、素数の振る舞いについてガウスの素数定理は漸近的にある数までの素数の個数を表している。そしてリーマンの素数公式はそれを厳密に表すように定式化しているのである。さらに素数公式は振動項により素数定理と実際の測定値との揺れを再現するとされており、そこにはゼータ関数の非自明な零点が寄与していた。即ち、ゼータ関数の非自明な零点の振る舞いがわかれば素数の分布をより精密にひも解くことができるというわけだ。
ついにここまで辿り着いた。この零点に対してリーマン予想の主張はこうだ。
「 ゼータ関数の非自明な零点は、すべて実部1/2の上に存在する。 」
これが数学の難問、リーマン予想であり、未だ未解決の問題だ。予想が正しければ素数の分布に対して非常に精密な評価が可能となるのである。予想に関していくつかわかっていることがあるが、直感的にわかりすい2つを記す。
・実部1/2の上には無限個の零点が存在する。
※少なくとも1/2上に無限個の零点があるのであって、1/2上”のみ”に存在するとは言っていない
・非自明な零点は実部0より大きく1より小さい範囲に存在する。
※零点の存在範囲を指しているのであって、1/2上”のみ”に存在するとは言っていない。
最後に
全3弾に渡って興味深い素数について解説してきた。特に第3弾である本記事では素数の最も今日深いお話であるリーマン予想について解説した。間違っている箇所など指摘をいただければどんどん修正をしていくので是非ご協力いただきたい。
リーマン予想について少しでも理解が深まってもらえれば嬉しいが、今までこういった数学の話に対して触れてこなかった方が興味を持ってくれることが本望だと考えている。ちなみに予想はミレニアム懸賞問題と呼ばれる数学界の最も重要な問題に指定されているもので、解ければ1億円の賞金がもらえる。100年以上も誰も解けていないので一筋縄とは行かないが、興味を持って数学の世界へチャレンジするのも面白い人生だと、私は思う。

コメント